Preskus Chi-Square z Excelom
Test Chi-Square v Excelu je najpogosteje uporabljen neparametrični test, ki se uporablja za primerjavo dveh ali več spremenljivk za naključno izbrane podatke. To je vrsta testa, ki se uporablja za ugotavljanje razmerja med dvema ali več spremenljivkami, to se uporablja v statistiki, ki je znana tudi kot P-vrednost Chi-Square, v Excelu nimamo vgrajene funkcije, lahko pa jo uporabimo formule za izvajanje testa hi-kvadrat v Excelu z uporabo matematične formule za test hi-kvadrat.
Vrste
- Chi-Square test za dobro prileganje
- Chi-Square test neodvisnosti dveh spremenljivk.
# 1 - Chi-Square test za dobro prileganje
Uporablja se za zaznavanje bližine vzorca, ki ustreza populaciji. Simbol testa Chi-Square je (2). To je vsota vseh ( Opaženo štetje - pričakovano štetje) 2 / pričakovano štetje.
- Kjer je k-1 stopnja svobode ali DF.
- Kjer je Oi opazovana frekvenca, je k kategorija, Ei pa pričakovana frekvenca.
Opomba: - Kakovost statističnega modela se nanaša na razumevanje, kako dobro vzorčni podatki ustrezajo nizu opazovanj.
Uporabe
- Kreditna sposobnost posojilojemalcev glede na njihove starostne skupine in osebna posojila
- Razmerje med uspešnostjo prodajalcev in opravljenim usposabljanjem
- Donosnost posamezne delnice in delnic sektorja, kot je farmacevtski ali bančni
- Kategorija gledalcev in vpliv televizijske kampanje.
# 2 - test Chi-Square za neodvisnost dveh spremenljivk
Uporablja se za preverjanje, ali so spremenljivke med seboj avtonomne ali ne. S stopnjami svobode (r-1) (c-1)
Kjer je Oi opazovana frekvenca, r število vrstic, c število stolpcev in Ei pričakovana frekvenca
Opomba: - Dve naključni spremenljivki se imenujeta neodvisni, če druga ne vpliva na porazdelitev verjetnosti ene spremenljivke.Uporabe
Preskus neodvisnosti je primeren za naslednje situacije:
- Obstaja ena kategorična spremenljivka.
- Obstajata dve kategorični spremenljivki, zato boste morali določiti razmerje med njima.
- Obstajajo navzkrižne tabele in treba je najti povezavo med dvema kategoričnima spremenljivkama.
- Obstajajo količinsko neopredeljive spremenljivke (na primer odgovori na vprašanja, na primer, ali zaposleni v različnih starostnih skupinah izbirajo različne vrste zdravstvenih načrtov?)
Kako narediti test Chi-Square v Excelu? (s primerom)
Vodja restavracije želi najti povezavo med zadovoljstvom strank in plačami ljudi, ki čakajo na mize. V tem bomo postavili hipotezo za preizkušanje hi-kvadrata
- Vzame naključni vzorec 100 strank, ki vprašajo, ali je bila storitev odlična, dobra ali slaba.
- Nato plače čakajočih kategorizira kot nizke, srednje in visoke.
- Predpostavimo, da je stopnja pomembnosti 0,05. Tu H0 in H1 označujeta neodvisnost in odvisnost kakovosti storitev od plač čakalnih miz.
- H 0 - kakovost storitev ni odvisna od plač ljudi, ki čakajo na mize.
- H 1 - Kakovost storitev je odvisna od plač ljudi, ki čakajo na mize.
- Njene ugotovitve so prikazane v spodnji tabeli:
Pri tem imamo 9 podatkovnih točk, imamo 3 skupine, od katerih je vsaka dobila drugačno sporočilo o plači, rezultat pa je podan spodaj.

Zdaj bomo prešteli vsoto vseh vrstic in stolpcev. To bomo storili s pomočjo formule, tj. SUM. Če seštejemo Odlično v stolpec skupaj, smo zapisali = SUM (B4: D4) in nato pritisnite tipko enter.

Tako bomo dobili 26 . Enako bomo izvedli z vsemi vrsticami in stolpci.

Za izračun stopnje svobode (DF) uporabimo (r-1) (c-1)
DF = (3-1) (3-1) = 2 * 2 = 4
- Obstajajo 3 kategorije storitev in 3 kategorije plač.
- Imamo 27 anketirancev s srednjo plačo (spodnja vrstica, srednja)
- Imamo 51 anketirancev z dobro storitvijo (zadnji stolpec, sredina)
Zdaj moramo izračunati pričakovane frekvence: -
Pričakovane frekvence lahko izračunamo po formuli: -
- Za izračun odličnosti bomo uporabili množenje skupnega z nizkim z vsoto odličnih, deljeno z N.
Recimo, da moramo izračunati za 1. vrstico in 1. stolpec (= B7 * E4 / B9 ) . To bo dalo pričakovano število strank, ki so glasovale za odlične storitve za plače ljudi, ki čakajo na tako nizko raven, tj .
- E 11 = - (32 * 26) / 100 = 8,32 , E 12 = 7,02 , E 13 = 10,66
- E 21 = 16,32 , E 22 = 13,77 , E 23 = 20,91
- E 31 = 7,36 , E 32 = 6,21 , E 33 = 9,41
Podobno moramo za vse narediti enako, formula pa je uporabljena v spodnjem diagramu.

Dobimo tabelo pričakovanih frekvenc, kot je navedeno spodaj: -

Opomba: - Predpostavimo, da je stopnja pomembnosti 0,05. Tu H0 in H1 označujeta neodvisnost in odvisnost kakovosti storitev od plač čakalnih miz.
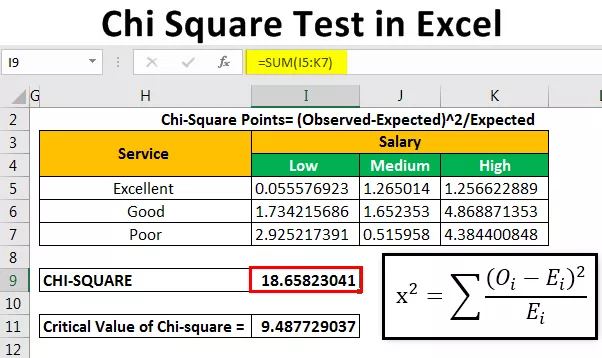
Po izračunu pričakovane frekvence bomo s pomočjo formule izračunali podatkovne točke hi-kvadrat.
Hi-kvadrat točke = (opaženo-pričakovano) 2 / pričakovano
Za izračun prve točke zapišemo = (B4-B14) 2 / B14.

Formulo bomo kopirali in prilepili v druge celice, da bo vrednost samodejno izpolnila.

Po tem bomo izračunali vrednost chi (Izračunana vrednost) z dodajanjem vseh vrednosti, podanih nad tabelo.

Vrednost Chi smo dobili kot 18.65823 .

Za izračun kritične vrednosti za to uporabimo tabelo kritičnih vrednosti hi-kvadrat, lahko uporabimo spodnjo formulo.
Ta formula vsebuje 2 parametra CHISQ.INV.RT (verjetnost, stopnja svobode).
Verjetnost je 0,05 in to je pomembna vrednost, ki nam bo pomagala ugotoviti, ali sprejeti ničelno hipotezo (H 0 ) ali ne.

Kritična vrednost hi-kvadrata je 9,487729037.

Zdaj bomo našli vrednost hi-kvadrat ali (P-vrednost) = CHITEST (dejanski_razpon, pričakovani_razpon)
Razpon od = CHITEST (B4: D6, B14: D16) .

Kot smo videli, je vrednost chi-testa ali vrednosti P = 0,00091723.

Izračunali smo vse vrednosti. Vrednosti hi-kvadrata (izračunane vrednosti) so pomembne le, če je njegova vrednost enaka ali večja od kritične vrednosti 9,48, tj. Kritična vrednost (tabelarična vrednost) mora biti višja od 18,65, da lahko sprejmete ničelno hipotezo (H 0 ) .
Ampak tukaj Izračunana vrednost > Tabelarična vrednost
X 2 (izračunano)> X 2 (tabelarično)
18,65> 9,48
V tem primeru bomo zavrnili nično hipotezo (H 0 ) in sprejemamo nadomestno (H 1 ) .
- Tudi vrednost P lahko uporabimo za napoved istega, tj. Če je vrednost P <= α (pomembna vrednost 0,05), bo Nultova hipoteza zavrnjena.
- Če je vrednost P> α , ničelne hipoteze ne zavrnite .
Tu je vrednost P (0,0009172) < α (0,05), zavrni H 0 , sprejme H 1
Iz zgornjega primera sklepamo, da je kakovost storitve odvisna od plač čakalcev.
Stvari, ki si jih je treba zapomniti
- Upošteva kvadrat standardne normalne spremenljivke.
- Oceni, ali se frekvence, opažene v različnih kategorijah, bistveno razlikujejo od frekvenc, pričakovanih v določenem nizu predpostavk.
- Določa, kako predpostavljena distribucija ustreza podatkom.
- Uporablja nepredvidene tabele (v tržnih raziskavah se te tabele imenujejo navzkrižni jezički).
- Podpira meritve na nominalni ravni.








