Sestavljena opredelitev
Sestavljanje je metoda izračunavanja obrestne mere, ki je dejansko obresti na obresti, pri čemer se obresti izračunajo na naložbo / začetno glavnico plus zaslužene obresti in druge ponovne naložbe, z drugimi besedami, zaslužene obresti se naberejo do zneska glavnice, odvisno od obdobja vloge ali posojila to je lahko mesečno, četrtletno ali letno
Poskusimo skozi nekaj osnovnih primerov razumeti, kaj se sestavlja in kako deluje
Top 4 primeri moči sestavljanja
Primer # 1
Oba Shane in Mark sta se odločila, da bosta vložila 1.000.000 USD, toda Shane se je odločil, da bo vlagal z enostavnimi obrestmi, medtem ko Mark deset let vlaga v obrestne obresti z 10% obrestmi. Poglejmo, kaj se bo zgodilo po desetih letih.
Rešitev:
Torej, izračun Shaneove naložbe bo -

Skupni znesek zaslužka = 200.000 USD
Z enostavnimi obrestmi bo Shane po 10 letih dobil 2.000.000 USD.
Izračun naložbe v znamko bo -

Skupni znesek zaslužka = 2,59,374 USD
Z obrestnimi merami se bodo Markove vrednosti naložb povečale na 2.599.774 USD.
Zdaj se je Shane odločil za naložbe po metodah mešanja, kot je Mark, in oba sta vložila 2.000.000 USD po stopnji 15%.
Izračun Shaneove naložbe bo -

Skupni znesek zaslužka = 8,09.111,55 USD
Shane vlaga 10 let in dobi končni znesek v višini 8,09.111,55 USD po stopnji 15%.
Izračun naložbe v znamko bo -

Skupni znesek zaslužka = 65,83.790,52 USD
Vendar je Mark dolgoročni vlagatelj potrpežljiv in vlaga 25 let, njegova vrednost naložbe pa naraste na 65.83.790,52 USD
Zgornji primer prikazuje moč mešanja. Daljši kot je naložbeni horizont, večja je eksponentna rast.
2. primer (tedensko)
Simon ima prihranke v višini 7500 ameriških dolarjev, za sinovski univerzitetni sklad, ki se bo po 15 letih šolal na fakulteti, pa se je odločil za naložbo v ameriške hranilnice. Cilj Simona je prihraniti 20.000 ameriških dolarjev, letna obrestna mera za ameriško varčevalno obveznico pa je 6%. Kakšna je prihodnja vrednost Simonovega denarja po 15 letih?
Rešitev:
Glede na to,
- Glavnica = 7500 USD
- Stopnja = 6% ali 0,06
- Časovno obdobje = 15 let.
- Kolikokrat je sestavljeno v letu n = 52 tednov
- Prihodnja vrednost =?
Torej, izračun prihodnje vrednosti bo -

Formula za tedensko mešanje je naslednja.
F = P (1 + r / n) n * t- F = 7500 USD (1 + 0,06 / 52) 52 * 15
- F = 7500 USD (1 + 0,001153846) 780
- F = 18.437,45 USD
Torej iz zgornjega izračuna je jasno, da Simonov cilj, da prihrani 20,00 USD, ne bo dosežen z zgornjimi metodami, vendar je bližje temu.
Metoda neprekinjenega mešanja
Zdaj poskusimo z zgornjim primerom s formulo za neprekinjeno sestavljanje.
Torej, izračun prihodnje vrednosti bo -

- F = 7500 ee 0,06 * 15
- F = 7500 e 0,9
- Prihodnja vrednost (F) = 18.447,02 USD
Zdaj tudi z neprekinjenim združevanjem Simonov cilj, da prihrani 20.000 dolarjev za univerzitetni sklad svojega sina, ne bo dosežen.
Poglejmo z mesečno sestavljeno formulo, koliko denarja je moral Simon vložiti, da bi dosegel svoj cilj, da bi v 15 letih prihranil 20.000 ameriških dolarjev s 6-odstotnim letnim prihodkom?
Torej, izračun prihodnje vrednosti bo -
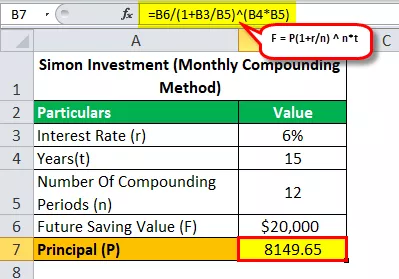
- 20.000 $ = P (1 + 0,06 / 12) 12 * 15
- P = 20.000 USD / (1 + 0,06 / 12) 12 * 15
- Glavnica (P) = 8149,65
Tako bomo z rešitvijo zgornje enačbe dobili odgovor v višini 8.149,65 USD (znesek, ki ga mora Simon vložiti, da bi v 15 letih prihranil 20.000 USD).
Primer # 3 (efektivni letni donos)
Recimo, da XYZ omejena banka daje 10% letno starejšim za fiksni depozit in tu domnevamo, da so bančne obresti četrtletno sestavljene kot vse druge banke. Izračunajte efektivni letni donos za 5, 7 in 10 let.
Rešitev:
Letni donos za 5 let:
- t = 5 let
- n = 4 (četrtletno sestavljeno)
- I = 10% letno
Torej A = (1 + 10% / 100/4) (5 * 4)
- A = (1 + 0,025) 20
- A = 1,6386
- I = 0,6386 v 5 letih
Efektivne obresti = 0,6386 / 5
Učinkovito I = 12,772% na leto
Letni donos za 7 let:
- t = 7 let
- n = 4 (četrtletno sestavljeno)
- I = 10% letno
Torej A = (1 + 10% / 100/4) (7 * 4)
- A = (1 + 0,025) 28
- A = 1,9965
- I = 1,9965 v 7 letih
- Učinkovito I = 0,9965 / 7
Učinkovito I = 14,236% na leto
Letni donos za 10 let:
- t = 10 let
- n = 4 (četrtletno sestavljeno)
- I = 10% letno
Torej A = (1 + 10% / 100/4) (10 * 4)
- A = (1 + 0,025) 40
- A = 2,685
- I = 1,685 v 10 letih
- Učinkovito I = 1.685 / 10
Učinkovito I = 16,85% na leto
Primer # 4 - (rente: prihodnja vrednost)
Vsak 3 mesece se vloži 1000 USD po 4,8% na leto, sestavljeno četrtletno. Koliko bo renta vredna čez 10 let?
Rešitev:
Ko torej rečemo, koliko bo renta vredna čez 10 let, moramo tukaj najti prihodnjo vrednost, in to pomembno, kajti kadar koli je primer rente, moramo videti, kaj moramo ugotoviti.
Torej, formula prihodnje vrednosti je
FV rente = P ((1+ r) n - 1 / r)- P = Periodično plačilo
- r = stopnja na obdobje
- n = število obdobij
Formula prihodnje vrednosti je torej
- Torej tukaj P = 1.000 USD
- r = 4,8% letno ali 0,048
- r (četrtletno) = 0,048 / 4
- r (četrtletno) = 0,012
- n = 10 let
- n (Število primerov mešanja) = 10 × 4 = 40
Torej, izračun FV rente bo -

Torej zdaj FV = 1000 USD (1 + 0,012) 40 -1 / 0,012)
Torej bomo z reševanjem zgornje enačbe dobili FV v višini 50.955,30 USD
Kolikšna bo torej renta čez 10 let in odgovor znaša 50.955,30 USD
Kot dodatek lahko iz zgornjega primera ugotovimo tudi, koliko obresti se zasluži v 10 letih.
Ker se vloži 40 krat 1000 dolarjev, je to skupna naložba (40 × 1000 dolarjev = 40.000 dolarjev).
Torej obresti = prihodnja vrednost - skupna naložba
- Obresti = 50.955,30 USD - 40.000 USD
- Obresti = 10.955,30 USD
Tu je torej pomembno razumeti, da lahko vlagatelji v rentah zaslužijo veliko obresti. V zgornjih posebnih primerih polog v višini 40.000 USD v zameno daje skupne obresti v višini 10.955,30 USD.
Opomba: Za podroben izračun lahko naložite zgoraj navedeno predlogo Excel.








